---

title: >-
[python&Advances mathematics Project # 1] draw multiple function images on a
canvas
type: categories
copyright: true
categories: Python
tags:

• Python
• 高等数学
• 图像绘制与可视化
• matplotlib

• 考研数学工具
  comments: true
  top: false
  abbrlink: 16eaace6
  date: 2020-08-04 17:00:49
  updated:

（1）Background and Application

We often need to draw a function image for our analysis in the learning and application of advanced mathematics, mathematical analysis and visualization and other scenarios. This can be easily achieved through Python3, which is much more portable and easy to use than MATLAB.

（2）lib

• matplotlib
• numpy

（3）General code

Demand analysis

We need a can in the function of the multiple function image is drawn with a picture at the same time, in order to show at the same time, contrast and analysis of law, so we first create the canvas, then according to the plot function is adopted to improve the rendering, according to the number of functions to achieve multiple functions at the same time drawing on the canvas, with design code is as follows：

#!usr/bin/env python
# -*- conding:utf-8 -*-
import matplotlib.pyplot as plt
from numpy import linspace,sqrt,sin,cos,tan,arctan,pi,exp

def plotFunction(x,y,x2 = None,y2 = None,x3=None,y3 = None):
    fig = plt.figure(num = 1,dpi = 120)
    ax = plt.subplot(111)

    # coordinate axes
    ax = plt.gca()  # get current axis
    ax.spines['right'].set_color('none') 
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.yaxis.set_ticks_position('left')
    # Set the coordinate axis of (0,0) at the center
    ax.spines['bottom'].set_position(('data', 0))  # Specifies that the bottom(that is, the X-axis specified) of the data setting is bound to the point 0 on the Y-axis
    ax.spines['left'].set_position(('data', 0))

    ax.plot(x,y,label = "first Fig",color ="blueviolet")
    if x2 is not None and y2 is not None:
        ax.plot(x2,y2,label = "Second Fig",color ="red")
    #ax.set_xlim(0,2)
    ax.set_xlabel("line",color='cyan')
    #plt.draw()
    plt.legend()
    plt.show()

Relevant parameters and image adjustment can be referred to the Matplotlib manual. This paper aims to provide a method and idea.

（4）Advanced Mathematical Function Test

Take the function f (x)= sine (1/x) as an example, first define a function and the scope of its definition:

x = linspace(-2*pi,2*pi,1000)
y = sin(1/x)

plotFunction(x,y)

For complex trigonometric functions, see the figure below：

If we want to know the graph of this function and how it differs from the sine of 1/x above, we just need to define it as follows:

x = linspace(-2*pi,2*pi,1000)
y = sin(1/x)
y2 = sqrt(x)*(x**3-4*cos(x)-sin(1))

plotFunction(x,y,x,y2)

This function can also be further extended, can be used to achieve the original function of the drawing, the drawing of the first derivative function and other functions.

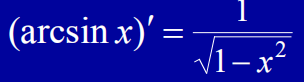
x = linspace(-pi/2,pi/2,1000)
y = arcsin(x)
y2 = 1/sqrt(1-x*x)

plotFunction(x,y,x,y2)

Other functions can be explored/improved on their own.